搜索算法

简单Minimax搜索

Minimax搜索

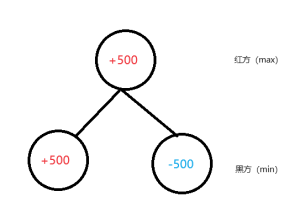
象棋属于零和博弈，有红方和黑方，双方的收益总和为0，一方的优势总是伴随着另一方的劣势。此时，我们可以使用Minimax进行搜索。

为了方便理解，我们暂且把Maximizing Player称为“红方”，把Minimizing Player称为“黑方”，我们的评估函数暂时返回的是相对于红方的分数（分高说明红方优势，分低说明红方劣势）。

博弈的双方都想让收益最大化，红方想让分数尽量高，黑方想让分数尽量低，这样就能最大程度上保证自己这方的优势，同时让对方占到的优势最小。

举个例子，红方在一个局面有两种走法。一种走法可以吃掉对方的车，此时的分数是+500，另一种走法是送掉自己的车，此时的分数是-500。红方当然会选择对自己有利的走法，即第一种，所以该节点的分数就是+500。

伪代码如下：

int minimax(int depth, bool isMaximizingPlayer) { // 层数, 是否红方
    if (depth == 0 || isGameOver()) { // 搜索到叶子节点或游戏结束，直接返回评估
        return evaluate();
    }

    if (isMaximizingPlayer) { // 如果当前是红方
        int maxEval = INT_MIN; // 初始化为尽量小的值，方便程序找出所有走法中分数的最大值
        for (Move move : getPossibleMoves()) { // 走法生成
            makeMove(move); // 走子
            int eval = minimax(depth - 1, false);
            undoMove(move); // 恢复到走子前的局面
            maxEval = std::max(maxEval, eval);
        }
        return maxEval;
    } else { // 如果当前是黑方
        int minEval = INT_MAX;  // 初始化为尽量大的值，方便程序找出所有走法中分数的最小值
        for (Move move : getPossibleMoves()) { // 走法生成
            makeMove(move); // 走子
            int eval = minimax(depth - 1, true);
            undoMove(move); // 恢复到走子前的局面
            minEval = std::min(minEval, eval);
        }
        return minEval;
    }
}

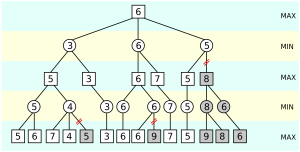
Alpha-Beta剪枝

上面实现的简单Minimax搜索，效率其实是很低的。我们这时就要引入一种新的搜索策略——Alpha-Beta剪枝，这种剪枝方法可以在不改变结果的前提下大大减少搜索的节点数。

Alpha-Beta剪枝

等待更新...