搜索算法:修订间差异
无编辑摘要 |
|||
| (未显示同一用户的7个中间版本) | |||
| 第104行: | 第104行: | ||
return minEval; | return minEval; | ||
} | } | ||
} | |||
</syntaxhighlight> | |||
== 继续简化,引入Negamax == | |||
前面我们的分数一直是相对于红方视角的,需要将红方和黑方分类讨论,这显然使代码复杂化了。为了解决这个问题,我们需要引入Negamax。 | |||
引入Negamax后,我们对双方可以使用同样的处理策略,省去了编写MIN方代码的必要性,但是评估函数需要改成相对于走子方的分数。 | |||
如果当前走子方是红方,需要返回相对于红方的分数;如果当前走子方是黑方,需要返回相对于黑方的分数。 | |||
由于我们把两种情况合并成了一种情况,判断红黑方的参数可以删去。 | |||
在搜索子节点的时候,我们需要从MAX层切换到MIN层,或者从MIN层切换到MAX层,应该如何做呢? | |||
在这里,我们继续举一个例子来说明。假设当前节点从父节点传下来的alpha值为5,beta值为8,说明最优走法的分数一定在5和8之间,接下来我们把分数视角切换到对手,最优走法的分数一定在-8和-5之间,-8和-5就分别是传递给子节点的alpha值和beta值。 | |||
所以,传给子节点的alpha和beta值应该是-beta和-alpha。 | |||
下面是引入Negamax后的伪代码: | |||
<syntaxhighlight lang="cpp"> | |||
int alphaBeta(int depth, int alpha, int beta) { | |||
if (depth == 0 || isGameOver()) { | |||
return evaluate(); | |||
} | |||
int maxEval = INT_MIN; // 初始化为负无穷,方便程序找出所有走法中分数的最大值 | |||
for (Move move : getPossibleMoves()) { // 走法生成 | |||
makeMove(move); // 走子 | |||
int eval = -alphaBeta(depth - 1, -beta, -alpha); // 向下一层搜索,获得该走法对应的子节点的分数 | |||
undoMove(move); // 恢复到走子前的局面 | |||
maxEval = std::max(maxEval, eval); | |||
alpha = std::max(alpha, eval); | |||
if (alpha >= beta) | |||
break; // Beta剪枝 | |||
} | |||
return maxEval; | |||
} | |||
</syntaxhighlight> | |||
有些资料上的代码可能是这样的: | |||
<syntaxhighlight lang="cpp"> | |||
int alphaBeta(int depth, int alpha, int beta) { | |||
if (depth == 0 || isGameOver()) { | |||
return evaluate(); | |||
} | |||
for (Move move : getPossibleMoves()) { | |||
makeMove(move); | |||
int val = -alphaBeta(depth - 1, -beta, -alpha); | |||
undoMove(move); | |||
if (val >= beta) { | |||
return beta; // Beta剪枝 | |||
} | |||
if (val > alpha) { | |||
alpha = val; // 更新Alpha的值 | |||
} | |||
} | |||
return alpha; | |||
} | |||
</syntaxhighlight> | |||
其实这两者是等价的,正常情况下,alpha<beta,所以alpha≥beta的情况只能是分数更新,导致alpha变大,发生Beta剪枝,所以直接和val进行比较也是一样的。 | |||
== 空步裁剪(Null Move Pruning)== | |||
一般来说,一个局面我方什么都不走(或者说走了一个“空步”),而是把走子权让给对方,我方是吃亏的。即最优走法的分数一般来说不会比走“空步”的分数低。 | |||
我们可以利用这一点编写一个剪枝策略——空步裁剪。空步裁剪是一种冒险策略,就是基于上面假设进行的,把比“空步”分数低的招法剪掉。 | |||
为了加快搜索,我们可以对“空步”搜索的层数额外减少R(一般是2-3)层。由于我们只关心“空步”的分数和beta相比是大还是小,所以应该用零窗口搜索([beta - 1, beta]),使Alpha-Beta剪枝在搜索空步时发挥的作用最大。 | |||
由于走子方互换,传递给子节点的alpha值和beta值也要按照之前的方法进行转换,也就是-beta和-beta + 1。 | |||
基于空步的分数≤最优走法的分数这个假设,如果返回的评估≤beta-1,说明后续该节点的alpha值有可能达不到beta,不进行剪枝;如果返回的评估≥beta,说明最优走法的分数也一定≥beta,也就是说后续alpha在更新的时候也会≥beta,可以直接进行剪枝。 | |||
然而一些局面并不满足之前我们提到过的假设,如国际象棋的迫移局面(Zguzwang),若使用空步裁剪,则会使引擎判断错误,于是我们可以设计一个“isNullMoveAllowed”函数判断是否满足空步裁剪的条件,尽量规避这种现象。 | |||
伪代码如下: | |||
<syntaxhighlight lang="cpp"> | |||
// R是空步裁剪搜索中额外减去的层数 | |||
const int R = 3; | |||
int alphaBeta(int depth, int alpha, int beta) { | |||
if (depth == 0 || isGameOver()) { | |||
return evaluate(); | |||
} | |||
// Null Move Pruning | |||
if (depth >= R + 1 && isNullMoveAllowed()) { | |||
makeNullMove(); // 走一步“空步” | |||
int nullMoveEval = -alphaBeta(depth - R - 1, -beta, -beta + 1); // 用[beta - 1, beta]进行搜索 | |||
undoNullMove(); // 恢复 | |||
if (nullMoveEval >= beta) { | |||
return beta; // 如果beta的值还不如走“空步”的分数高,就直接剪掉 | |||
} | |||
} | |||
int value = INT_MIN; | |||
for (Move move : getPossibleMoves()) { // 走法生成 | |||
makeMove(move); // 走棋 | |||
value = std::max(value, -alphaBeta(depth - 1, -beta, -alpha)); | |||
undoMove(move); // 恢复 | |||
alpha = std::max(alpha, value); | |||
if (alpha >= beta) { | |||
break; // Beta剪枝 | |||
} | |||
} | |||
return value; | |||
} | |||
</syntaxhighlight> | |||
== PVS(主要变例搜索) == | |||
PVS是对Alpha-Beta剪枝的增强,可以提高Alpha-Beta剪枝的效率。简单来说,PVS先对第一个子节点进行[alpha, beta]的全窗口搜索,再对剩余子节点使用[alpha, alpha+1]的零窗口搜索。零窗口搜索结束后,如果该节点搜索返回的评估在(alpha, beta)之间,说明该节点有希望,于是继续进行一次全窗口搜索。如果返回的评估超出了(alpha, beta),说明这个节点必然会被剪枝。 | |||
伪代码如下: | |||
<syntaxhighlight lang="cpp"> | |||
int alphaBeta(int depth, int alpha, int beta) { | |||
if (depth == 0 || isGameOver()) { | |||
return evaluate(); | |||
} | |||
int maxEval = INT_MIN; // 初始化为负无穷,方便程序找出所有走法中分数的最大值 | |||
bool firstChild = true; // 标记是否为第一个子节点 | |||
for (const Move& move : getPossibleMoves()) { // 走法生成 | |||
makeMove(move); // 走子 | |||
int eval; | |||
if (firstChild) { | |||
// 对第一个子节点使用全窗口搜索 | |||
eval = -alphaBeta(depth - 1, -beta, -alpha); | |||
firstChild = false; | |||
} else { | |||
// 对剩余子节点使用零窗口搜索 | |||
eval = -alphaBeta(depth - 1, -alpha - 1, -alpha); | |||
if (eval > alpha && eval < beta) { | |||
// 如果零窗口搜索未能确定性地剪枝,则进行全窗口重新搜索 | |||
eval = -alphaBeta(depth - 1, -beta, -eval); | |||
} | |||
} | |||
undoMove(move); // 恢复到走子前的局面 | |||
maxEval = std::max(maxEval, eval); | |||
alpha = std::max(alpha, eval); | |||
if (alpha >= beta) { | |||
break; // Beta 剪枝 | |||
} | |||
} | |||
return maxEval; | |||
} | |||
</syntaxhighlight> | |||
注:为了简化代码,这里并未加入空步裁剪,后文也是单独介绍某种方法,而不是叠加在一起。 | |||
== 静态搜索 == | |||
静态搜索(Quiescent Search)可以用来克服水平面效应。一般来说发生互相吃子,评估函数会发生剧烈变化,引入静态搜索,可以返回一个更加稳定的评估值。引入静态评估后,达到叶子节点时,我们不直接返回评估函数的值,而是进行一次静态搜索,继续探索吃子的走法。 | |||
伪代码如下: | |||
<syntaxhighlight lang="cpp"> | |||
int qsearch(int alpha, int beta) { | |||
int standPat = evaluate(); // 当前局面不做任何动作的评估值 | |||
if (standPat >= beta) { | |||
return beta; // 剪枝 | |||
} | |||
if (alpha < standPat) { | |||
alpha = standPat; // 更新 alpha | |||
} | |||
for (Move move : getPossibleCaptures()) { // 只考虑吃子的走法 | |||
makeMove(move); | |||
int eval = -qsearch(-beta, -alpha); // 静态搜索下一层 | |||
undoMove(move); | |||
if (eval >= beta) { | |||
return beta; // 剪枝 | |||
} | |||
if (eval > alpha) { | |||
alpha = eval; // 更新 alpha | |||
} | |||
} | |||
return alpha; | |||
} | |||
int alphaBeta(int depth, int alpha, int beta) { | |||
if (depth == 0 || isGameOver()) { | |||
return qsearch(alpha, beta); // 在深度为0或游戏结束时进入静态搜索 | |||
} | |||
int maxEval = INT_MIN; // 初始化为负无穷 | |||
for (Move move : getPossibleMoves()) { // 生成所有走法 | |||
makeMove(move); // 执行走法 | |||
int eval = -alphaBeta(depth - 1, -beta, -alpha); // 递归搜索 | |||
undoMove(move); // 撤销走法 | |||
maxEval = std::max(maxEval, eval); | |||
alpha = std::max(alpha, eval); | |||
if (alpha >= beta) { | |||
break; // Beta剪枝 | |||
} | |||
} | |||
return maxEval; | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
2024年10月2日 (三) 15:48的最新版本
简单Minimax搜索
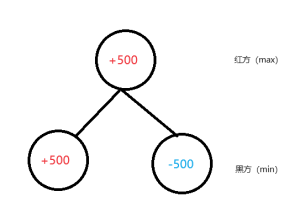
象棋属于零和博弈,有红方和黑方,双方的收益总和为0,一方的优势总是伴随着另一方的劣势。此时,我们可以使用Minimax进行搜索。
为了方便理解,我们暂且把Maximizing Player称为“红方”,把Minimizing Player称为“黑方”(实际上则不一定),我们的评估函数暂时返回的是相对于红方的分数(分高说明红方优势,分低说明红方劣势)。
博弈的双方都想让收益最大化,红方想让分数尽量高,黑方想让分数尽量低,这样就能最大程度上保证自己这方的优势,同时让对方占到的优势最小。
举个例子,红方在一个局面有两种走法。一种走法可以吃掉对方的车,此时的分数是+500,另一种走法是送掉自己的车,此时的分数是-500。红方当然会选择对自己有利的走法,即第一种,所以该节点的分数就是+500。
伪代码如下:
int minimax(int depth, bool isMaximizingPlayer) { // 层数, 是否红方
if (depth == 0 || isGameOver()) { // 搜索到叶子节点或游戏结束,直接返回评估
return evaluate();
}
if (isMaximizingPlayer) { // 如果当前是红方
int maxEval = INT_MIN; // 初始化为负无穷,方便程序找出所有走法中分数的最大值
for (Move move : getPossibleMoves()) { // 走法生成
makeMove(move); // 走子
int eval = minimax(depth - 1, false); // 向下一层搜索,获得该走法对应的子节点的分数
undoMove(move); // 恢复到走子前的局面
maxEval = std::max(maxEval, eval);
}
return maxEval;
} else { // 如果当前是黑方
int minEval = INT_MAX; // 初始化为正无穷,方便程序找出所有走法中分数的最小值
for (Move move : getPossibleMoves()) { // 走法生成
makeMove(move); // 走子
int eval = minimax(depth - 1, true); // 向下一层搜索,获得该走法对应的子节点的分数
undoMove(move); // 恢复到走子前的局面
minEval = std::min(minEval, eval); // 取最小值
}
return minEval;
}
}
Alpha-Beta剪枝的过程介绍
上面实现的简单Minimax搜索,效率其实是很低的。我们这时就要引入一种新的搜索策略——Alpha-Beta剪枝,这种剪枝方法可以在不改变结果的前提下大大减少搜索的节点数。
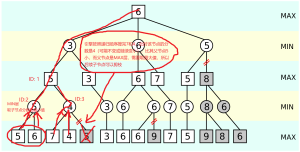
上文我们提到过,红方的目的是使得分尽量高,也就是说当前节点的分数是所有子节点分数的最大值,黑方则相反。
参考右图,我们可以举个例子说明一下Alpha-Beta剪枝的原理。
引擎搜完叶子节点的5和6,可以推断出这两个节点的父节点(图中ID:2)的分数是min(5,6)=5。这个节点的父节点在MAX层上(图中ID:1),是取其子节点分数的最大值,所以它的分数至少是5。子节点的分数只有>5才有搜下去的必要,否则不会比“ID:2”这一路线更优。
接下来我们继续搜索“ID:3”这一路线,搜完叶子节点的“7”和“4”之后,由于“ID:3”处在MIN层,其分数是取其子节点分数的最小值,所以这个节点的分数必然≤4,不可能比“ID:2”这一条路线更优,没有再搜下去的必要了,我们可以把后续的子节点(即灰色的5)剪掉。
其它灰色的部分也是同理,大家可自行按照上面的步骤推断。
根据理论推断是会了,但这仍是纸上谈兵,如何编写相关代码实现该功能呢?且听下回分解。
Alpha-Beta剪枝的代码实现
为了用代码实现Alpha-Beta剪枝,我们需要引入alpha和beta两个量,alpha是红方能保证至少获得的分数,beta是黑方能保证至多获得的分数(这里的分数都是从红方视角看的)。也就是说,最优走法的分数必然≥alpha而且≤beta。
在最开始调用“alphaBeta”函数的时候,我们应该把alpha设为负无穷,把beta设为正无穷。
当我们搜索一个节点的时候,我们需要接受从父节点传来的alpha和beta值,接着判断该节点处于MAX层还是MIN层。
这里还是举一个例子方便读者理解,假设我们处于MAX层(即红方),父节点传递的alpha值是5,beta值是8。
因为当前节点的分数是从子节点的分数中取最大值得到的,所以我们在搜索的时候可以保证当前节点的分数≥子节点的分数,应该根据子节点的分数更新alpha的值。如果我们此时搜到一个子节点,分数为10,此时当前节点的分数必定≥10。但我们不要忘了,上一层是MIN,取的是子节点中的最小分数。若当前节点的分数超过了beta,必然不会比其父节点之前搜过的某个子节点分数低,不会被父节点采纳;若当前节点的分数等于beta,必然不会比其父节点之前搜过的某个子节点更优。我们可以直接使用break跳出循环,进行Beta剪枝,同时返回目前搜过的子节点的最大分数(目前的搜索代码中,这里返回值不重要,只需要保证该节点不被父节点采纳即可)。
判断当前节点的分数是否≥beta,可以等同于判断alpha≥beta,因为alpha就是按照子节点的分数通过取最大值进行更新的。
MIN层同理,这里不再赘述。
伪代码如下:
int alphaBeta(int depth, int alpha, int beta, bool isMaximizingPlayer) {
if (depth == 0 || isGameOver()) {
return evaluate();
}
if (isMaximizingPlayer) { // 如果当前是红方
int maxEval = INT_MIN; // 初始化为负无穷,方便程序找出所有走法中分数的最大值
for (Move move : getPossibleMoves()) { // 走法生成
makeMove(move); // 走子
int eval = alphaBeta(depth - 1, alpha, beta, false); // 向下一层搜索,获得该走法对应的子节点的分数
undoMove(move); // 恢复到走子前的局面
maxEval = std::max(maxEval, eval); // 取最大值
alpha = std::max(alpha, eval);
if (beta <= alpha)
break; // Beta剪枝
}
return maxEval;
} else { // 如果当前是黑方
int minEval = INT_MAX; // 初始化为正无穷,方便程序找出所有走法中分数的最小值
for (Move move : getPossibleMoves()) { // 走法生成
makeMove(move); // 走子
int eval = alphaBeta(depth - 1, alpha, beta, true); // 向下一层搜索,获得该走法对应的子节点的分数
undoMove(move); // 恢复到走子前的局面
minEval = std::min(minEval, eval); // 取最小值
beta = std::min(beta, eval);
if (beta <= alpha)
break; // Alpha剪枝
}
return minEval;
}
}
继续简化,引入Negamax
前面我们的分数一直是相对于红方视角的,需要将红方和黑方分类讨论,这显然使代码复杂化了。为了解决这个问题,我们需要引入Negamax。
引入Negamax后,我们对双方可以使用同样的处理策略,省去了编写MIN方代码的必要性,但是评估函数需要改成相对于走子方的分数。
如果当前走子方是红方,需要返回相对于红方的分数;如果当前走子方是黑方,需要返回相对于黑方的分数。
由于我们把两种情况合并成了一种情况,判断红黑方的参数可以删去。
在搜索子节点的时候,我们需要从MAX层切换到MIN层,或者从MIN层切换到MAX层,应该如何做呢?
在这里,我们继续举一个例子来说明。假设当前节点从父节点传下来的alpha值为5,beta值为8,说明最优走法的分数一定在5和8之间,接下来我们把分数视角切换到对手,最优走法的分数一定在-8和-5之间,-8和-5就分别是传递给子节点的alpha值和beta值。
所以,传给子节点的alpha和beta值应该是-beta和-alpha。
下面是引入Negamax后的伪代码:
int alphaBeta(int depth, int alpha, int beta) {
if (depth == 0 || isGameOver()) {
return evaluate();
}
int maxEval = INT_MIN; // 初始化为负无穷,方便程序找出所有走法中分数的最大值
for (Move move : getPossibleMoves()) { // 走法生成
makeMove(move); // 走子
int eval = -alphaBeta(depth - 1, -beta, -alpha); // 向下一层搜索,获得该走法对应的子节点的分数
undoMove(move); // 恢复到走子前的局面
maxEval = std::max(maxEval, eval);
alpha = std::max(alpha, eval);
if (alpha >= beta)
break; // Beta剪枝
}
return maxEval;
}
有些资料上的代码可能是这样的:
int alphaBeta(int depth, int alpha, int beta) {
if (depth == 0 || isGameOver()) {
return evaluate();
}
for (Move move : getPossibleMoves()) {
makeMove(move);
int val = -alphaBeta(depth - 1, -beta, -alpha);
undoMove(move);
if (val >= beta) {
return beta; // Beta剪枝
}
if (val > alpha) {
alpha = val; // 更新Alpha的值
}
}
return alpha;
}
其实这两者是等价的,正常情况下,alpha<beta,所以alpha≥beta的情况只能是分数更新,导致alpha变大,发生Beta剪枝,所以直接和val进行比较也是一样的。
空步裁剪(Null Move Pruning)
一般来说,一个局面我方什么都不走(或者说走了一个“空步”),而是把走子权让给对方,我方是吃亏的。即最优走法的分数一般来说不会比走“空步”的分数低。
我们可以利用这一点编写一个剪枝策略——空步裁剪。空步裁剪是一种冒险策略,就是基于上面假设进行的,把比“空步”分数低的招法剪掉。
为了加快搜索,我们可以对“空步”搜索的层数额外减少R(一般是2-3)层。由于我们只关心“空步”的分数和beta相比是大还是小,所以应该用零窗口搜索([beta - 1, beta]),使Alpha-Beta剪枝在搜索空步时发挥的作用最大。
由于走子方互换,传递给子节点的alpha值和beta值也要按照之前的方法进行转换,也就是-beta和-beta + 1。
基于空步的分数≤最优走法的分数这个假设,如果返回的评估≤beta-1,说明后续该节点的alpha值有可能达不到beta,不进行剪枝;如果返回的评估≥beta,说明最优走法的分数也一定≥beta,也就是说后续alpha在更新的时候也会≥beta,可以直接进行剪枝。
然而一些局面并不满足之前我们提到过的假设,如国际象棋的迫移局面(Zguzwang),若使用空步裁剪,则会使引擎判断错误,于是我们可以设计一个“isNullMoveAllowed”函数判断是否满足空步裁剪的条件,尽量规避这种现象。
伪代码如下:
// R是空步裁剪搜索中额外减去的层数
const int R = 3;
int alphaBeta(int depth, int alpha, int beta) {
if (depth == 0 || isGameOver()) {
return evaluate();
}
// Null Move Pruning
if (depth >= R + 1 && isNullMoveAllowed()) {
makeNullMove(); // 走一步“空步”
int nullMoveEval = -alphaBeta(depth - R - 1, -beta, -beta + 1); // 用[beta - 1, beta]进行搜索
undoNullMove(); // 恢复
if (nullMoveEval >= beta) {
return beta; // 如果beta的值还不如走“空步”的分数高,就直接剪掉
}
}
int value = INT_MIN;
for (Move move : getPossibleMoves()) { // 走法生成
makeMove(move); // 走棋
value = std::max(value, -alphaBeta(depth - 1, -beta, -alpha));
undoMove(move); // 恢复
alpha = std::max(alpha, value);
if (alpha >= beta) {
break; // Beta剪枝
}
}
return value;
}
PVS(主要变例搜索)
PVS是对Alpha-Beta剪枝的增强,可以提高Alpha-Beta剪枝的效率。简单来说,PVS先对第一个子节点进行[alpha, beta]的全窗口搜索,再对剩余子节点使用[alpha, alpha+1]的零窗口搜索。零窗口搜索结束后,如果该节点搜索返回的评估在(alpha, beta)之间,说明该节点有希望,于是继续进行一次全窗口搜索。如果返回的评估超出了(alpha, beta),说明这个节点必然会被剪枝。
伪代码如下:
int alphaBeta(int depth, int alpha, int beta) {
if (depth == 0 || isGameOver()) {
return evaluate();
}
int maxEval = INT_MIN; // 初始化为负无穷,方便程序找出所有走法中分数的最大值
bool firstChild = true; // 标记是否为第一个子节点
for (const Move& move : getPossibleMoves()) { // 走法生成
makeMove(move); // 走子
int eval;
if (firstChild) {
// 对第一个子节点使用全窗口搜索
eval = -alphaBeta(depth - 1, -beta, -alpha);
firstChild = false;
} else {
// 对剩余子节点使用零窗口搜索
eval = -alphaBeta(depth - 1, -alpha - 1, -alpha);
if (eval > alpha && eval < beta) {
// 如果零窗口搜索未能确定性地剪枝,则进行全窗口重新搜索
eval = -alphaBeta(depth - 1, -beta, -eval);
}
}
undoMove(move); // 恢复到走子前的局面
maxEval = std::max(maxEval, eval);
alpha = std::max(alpha, eval);
if (alpha >= beta) {
break; // Beta 剪枝
}
}
return maxEval;
}
注:为了简化代码,这里并未加入空步裁剪,后文也是单独介绍某种方法,而不是叠加在一起。
静态搜索
静态搜索(Quiescent Search)可以用来克服水平面效应。一般来说发生互相吃子,评估函数会发生剧烈变化,引入静态搜索,可以返回一个更加稳定的评估值。引入静态评估后,达到叶子节点时,我们不直接返回评估函数的值,而是进行一次静态搜索,继续探索吃子的走法。
伪代码如下:
int qsearch(int alpha, int beta) {
int standPat = evaluate(); // 当前局面不做任何动作的评估值
if (standPat >= beta) {
return beta; // 剪枝
}
if (alpha < standPat) {
alpha = standPat; // 更新 alpha
}
for (Move move : getPossibleCaptures()) { // 只考虑吃子的走法
makeMove(move);
int eval = -qsearch(-beta, -alpha); // 静态搜索下一层
undoMove(move);
if (eval >= beta) {
return beta; // 剪枝
}
if (eval > alpha) {
alpha = eval; // 更新 alpha
}
}
return alpha;
}
int alphaBeta(int depth, int alpha, int beta) {
if (depth == 0 || isGameOver()) {
return qsearch(alpha, beta); // 在深度为0或游戏结束时进入静态搜索
}
int maxEval = INT_MIN; // 初始化为负无穷
for (Move move : getPossibleMoves()) { // 生成所有走法
makeMove(move); // 执行走法
int eval = -alphaBeta(depth - 1, -beta, -alpha); // 递归搜索
undoMove(move); // 撤销走法
maxEval = std::max(maxEval, eval);
alpha = std::max(alpha, eval);
if (alpha >= beta) {
break; // Beta剪枝
}
}
return maxEval;
}